The discrete approximation of the diffusion phenomenon of ink spread in a river.

The discrete approximation of the diffusion phenomenon of ink spread in a river.

Associate professor (Probability Theory and Geometry)
ISHIWATA Satoshi

In mathematics, it is often encountered that "existence is known, but the specific form is unknown." The problem of "how ink diffuses when dropped into a river" can be shown to have a unique solution under appropriate assumptions based on the general theory of diffusion equations. However, determining how the ink spreads in complex flow situations, such as rivers with twists and turns or where water enters and exits, is a very challenging problem.

In a recently published paper co-authored with Professor Hiroshi Kawabi from Keio University, I proposed one solution to this problem by discretizing the river into smaller segments. I demonstrated that the distribution of ink can be approximated using the solutions of discrete equations on this discrete model. In recent years, advancements in computing power have made it easier to obtain discrete approximations of solutions even for such problems. However, a fundamental theory that guarantees that the approximate solutions accurately reflect the actual solutions plays a crucial role behind the scenes.

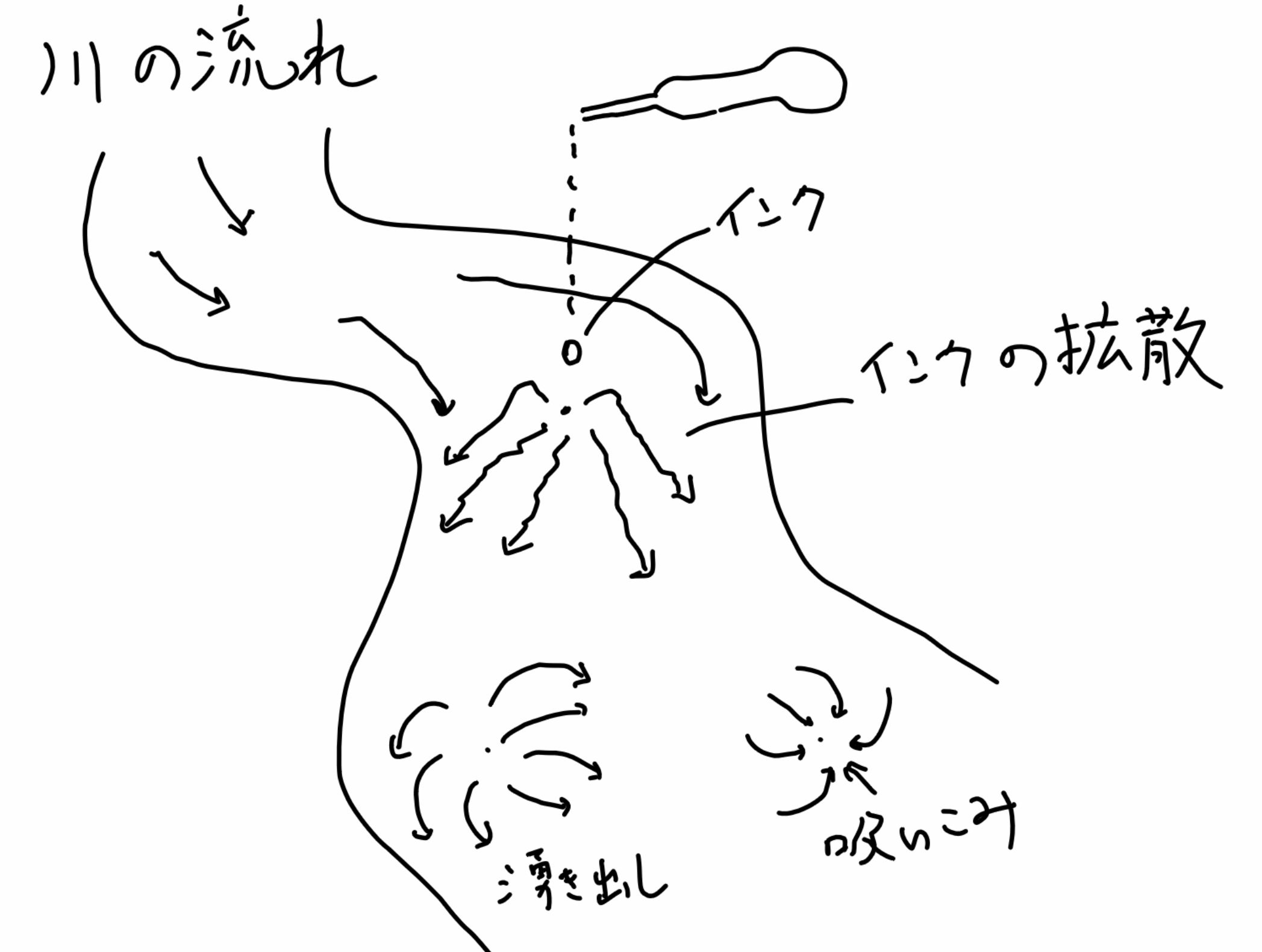
▲The diffusion of ink dropped into a river.

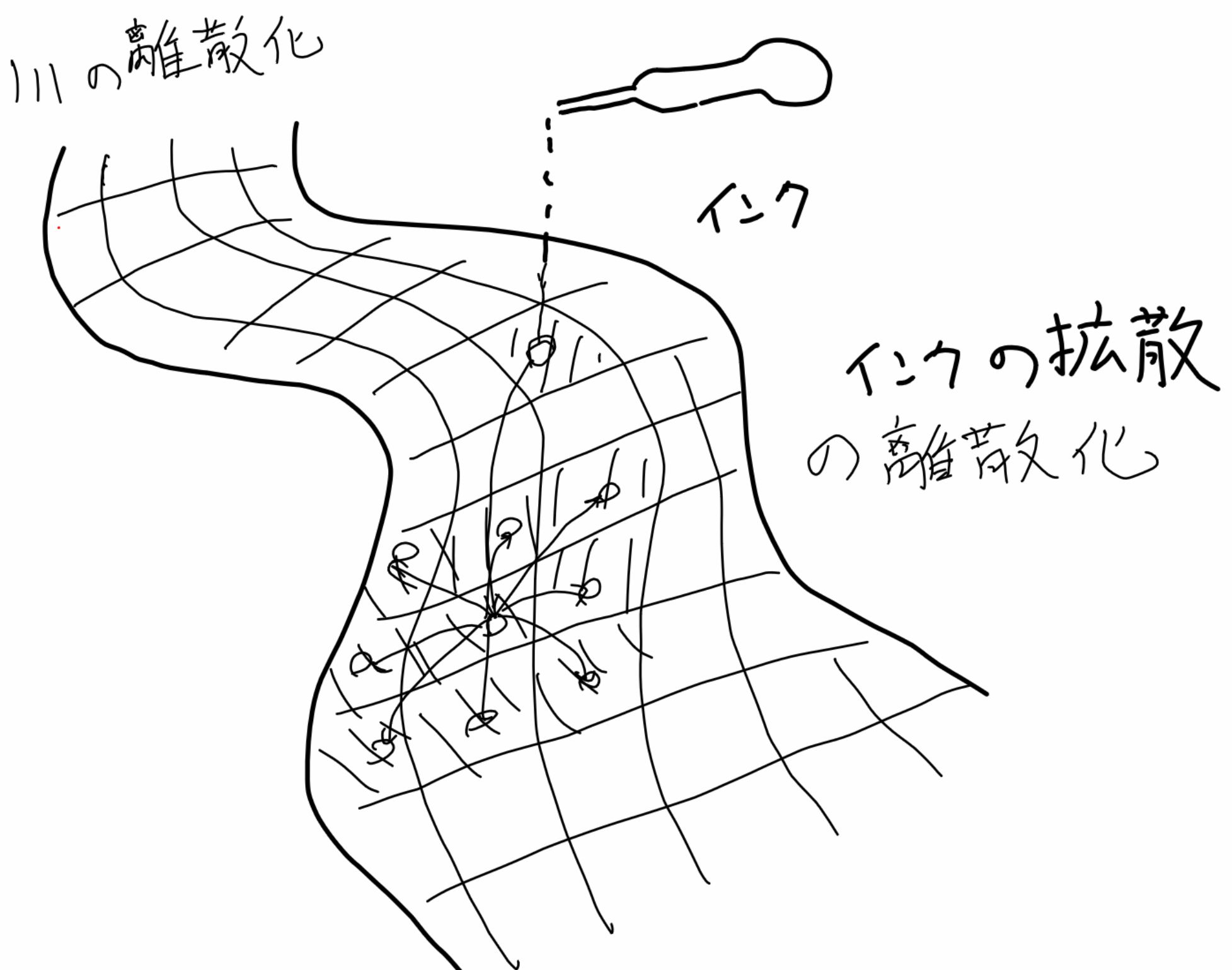
▲Discretization of ink diffusion

▲The collaborative research with Professor Kawabi.