研究するひと #09
中村誠
数学的美しさを求め挑む、
難解な偏微分方程式。
2018.04.30


研究するひと #09
中村誠
2018.04.30

自然現象から株価、保険、通信暗号まで、さまざまな分野で数学理論が役に立つと注目されている。しかし、関数方程式論を専門とする中村誠教授は、そんな実用性だけでなく、自然科学の言語としての数学に魅力があるという。数学的美しさとは何なのか? その難解な世界を垣間見てみよう。
複雑な数式に挑む中村先生の数学研究者としてのルーツを探ると、意外にも数学を苦痛と感じている中学・高校生時代があった。四則演算やユークリッド幾何、三段論法などを誰もが「正しい」と疑いもなく受け入れている現実に対して、中村先生はその正しい理由が気になり、いろいろ考えて納得しようとしたものの確たる理由が見つからなかったという過去がある。これらは数学の基本であったため、それまで自身の足元にあった固い地面が急に深い海の底に直結するような恐れまで抱いたという。大学進学後に、ロバチェフスキーやカントール、ゲーデルなど歴代の数学者たちが同じことを考え、学問として体系立っていることを知って驚くとともに、ようやく安心するに至った。これらの問題は、取り組んだ数学者が精神的に病むほどに難しく、そもそもの認識から疑わなければならないものだったのだ。特にゲーデルは数学が「真実」を述べている訳ではなく、「完全なものではない」ことを示しており、人間を取り巻く全ての解明に挑戦しているような気がした、と中村先生は述懐する。

文献を読み込み、背景にある数学的構造を明らかにし、新しい仕組みを作り出すのが中村先生の研究スタイル。
一方で、1980年代には宇宙の数学モデルが数多く研究されていたこともあり、中村先生は宇宙の成り立ちや時空の構造にある数学的美しさに興味を持つようになった。大学4年時に、数学基礎論か偏微分方程式論の研究かで迷った際には、やはり自然現象の背景にある数学的構造への関心が高かったため、偏微分方程式論を選択した。つまり、中村先生のモチベーションは、数学や物理が好きというよりも、「自然現象を理解できるシンプルで数学的に美しい理論が知りたい」という探求心にあったのだ。
数学の研究のあり方は、極めて孤独だと言われている。特に、中村先生は理論系で基本的に文献を読み込み、背景にある数学的構造を明らかにして、新しい仕組みを作り出すことに多くの時間を費やすため、この期間は人との交流がほとんどない。相手は「自然」で、しかも「自然の言語」である数学で表現しなければならないため、厳密性が求められるのだ。ほんの僅かな小さな論理の綻びが、結果全てを台無しにしてしまう。研究は、一人で朝から晩まで数か月単位で森の中をさまよい、時々見晴らしの良い丘に行き当たって自分の位置を確認し、より良い場所へ向かう、そんな行程に似ているという。だからこそ、研究内容の発表や外部資金の獲得の際に、外部研究者からの厳しい評価は重要で、否定的であっても自分の位置を知るのに役立つという。

数学の研究は孤独な面が多い。ノートに向かって黙々と数式やグラフなどを書き、考えを整理する中村先生。
逆に、これまでの研究から新しい考えがまとまってきて、学術誌での発表に値するアイデアが頭に浮かび、それを厳密に検証して、その中に数学的美しさを感じた時が最も嬉しい瞬間だという。例えば、非線形波動方程式の解の存在証明では、非線形項の構造とエネルギー評価をうまく組み合わせると、僅か3つのステップで証明ができることに気づいた時。祈るような気持ちで検証した数日間が今でも鮮明な記憶となって甦るそうだ。最近では、半線形拡散方程式と半線形シュレディンガー方程式の、アインシュタイン方程式を基礎にした統一導出の研究でアイデアが浮かんだ時が嬉しかったという。
現在は、そのアインシュタイン方程式から導かれる、動的時空における非線形偏微分方程式を研究テーマとしている。この場合、変数係数の非線形偏微分方程式を扱うが、定数係数の場合と比べて数学的な困難が大きいため、しばらくは方法論の構築に時間をかける予定だ。この困難の克服のためには、数値シミュレーションによる解の挙動の把握も有効であるため、学外の専門家と共に取り組んでいる。

もちろん、パソコンに向かって作業をすることもしばしば。論文を書いたり、グラフ化したり、文献を調べたり。
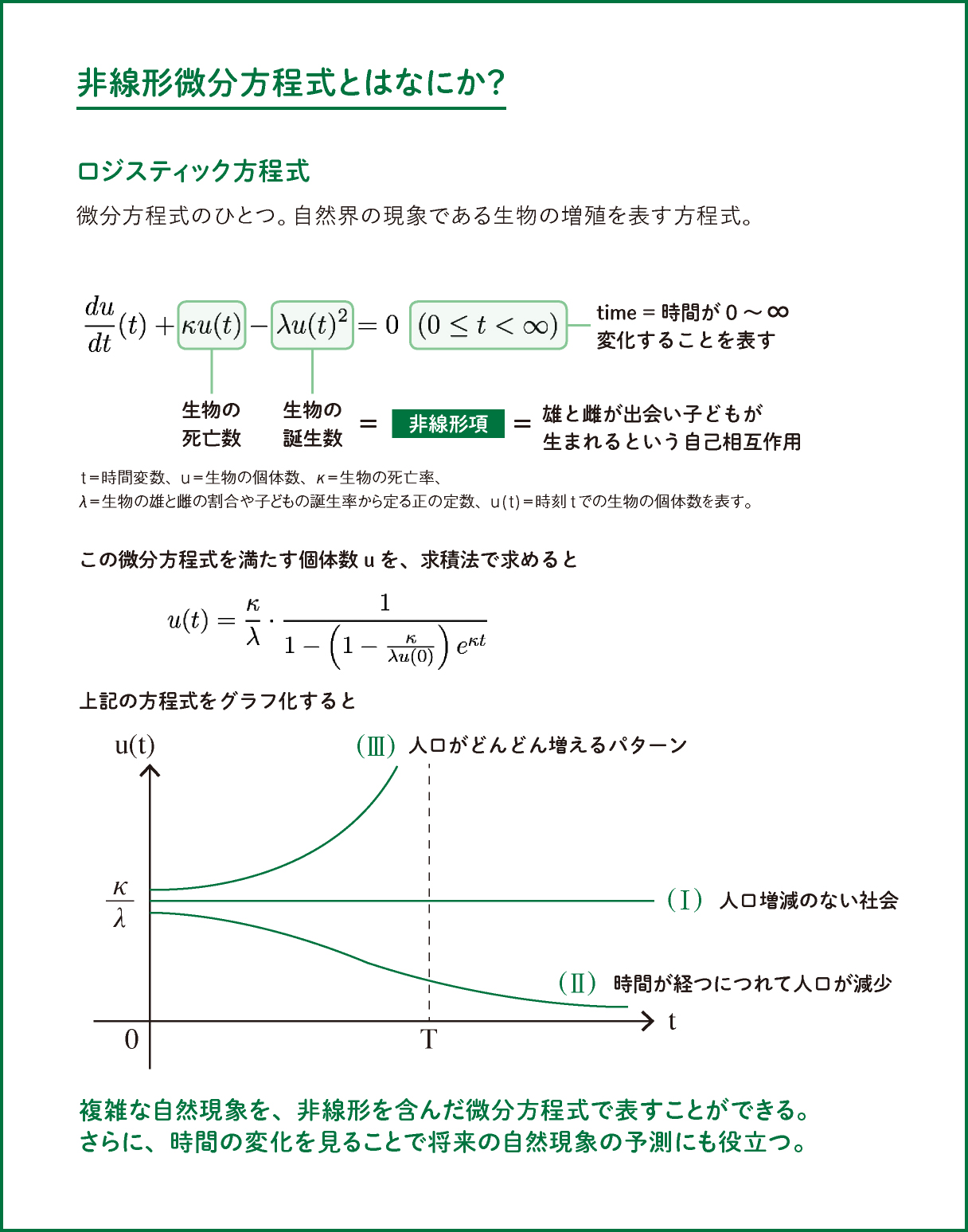
相互作用と呼ばれる非線形性を含んだ微分方程式をテーマとする中村先生の研究の核心に迫るその前に、まずは「非線形微分方程式」とは何かを、生物の増殖モデルであるロジスティック方程式を例に説明しよう(上記の数式とグラフを参照)。ここでtは時間変数、uは生物の個体数、κは死亡率を表し、λは生物の雄と雌の割合や子どもの誕生率から定まる正の定数である。この方程式の左辺の第3項λu(t)²は生物の雄と雌が出会い、子どもが生まれるという自己相互作用を表す。この微分方程式を満たすuは、求積法と呼ばれる方法により求められた式をグラフ化すると、(Ⅰ)(Ⅱ)(Ⅲ)の3パターンが描かれ、t=0での個体数がκ/λであれば、個体数uは増えることも減ることもない直線(Ⅰ)、κ/λより小さければ、個体数uは減っていき、最終的には絶滅(Ⅱ)、κ/λより大きければ、個体数uは有限時間で無限大(Ⅲ)になる。これを人間に置き換えると、人口の増減を示し、少子化対策の必要性や食料や資源の奪い合いが起こる可能性を示唆する。このように非線形を考えることで多くの現象を記述することができ、微分方程式を用いて、その現象の将来を予測することができる。
さらに、上記の非線形微分方程式が時間微分のみであるのに対して、中村先生の研究では、空間微分をともに含んだ非線形偏微分方程式を扱っている。非線形偏微分方程式を考えることにより、熱やエネルギーの拡散、音波や電磁波などの波の伝播、量子力学における確率密度分布など、自然現象の多くを記述することが可能になる。特に、方程式の「解の存在と一意性」について研究しており、「解の存在」は、方程式が記述する現象が存在することに、また「解の一意性」は、現象の起り方がただ一通りであることに対応する。
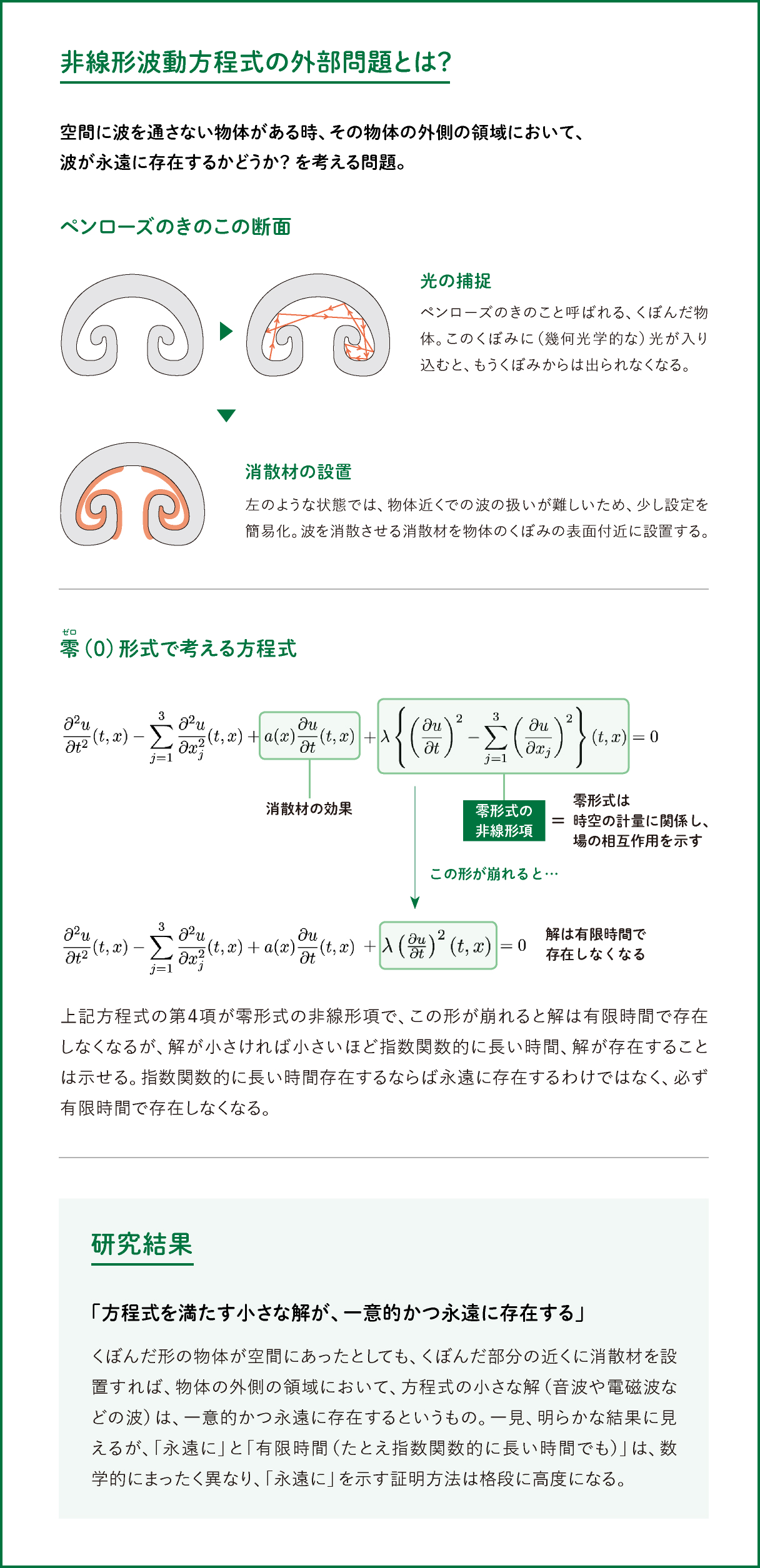
さて、ここからが本題。中村先生の研究の一つ、非線形波動方程式の外部問題について解説しよう(上記の数式を参照)。これは空間に波を通さない物体がある時、その物体の外側の領域において波が永遠に存在するかどうかを考える問題だ。物体の形の例としては、「ペンローズのきのこ」と呼ばれる、くぼんだ物体を考える。このくぼみに(幾何光学的な)光が入り込むと、永久にくぼみから出られない。このままでは、物体の近くでの波の扱いが難しいので、少し設定を簡易化し、波を消散させるような材料(消散材)を物体のくぼみの表面付近に設置する。また、非線形としては、零(ゼロ)形式と呼ばれる特殊な構造を持つものを考える。上記の方程式の左辺の第3項が消散材の設置に相当し、左辺第4項が零形式の非線形項。零形式は時空の計量に関係しており、この形が崩れると、解は有限時間で存在しなくなる。有限時間で存在しなくなると言っても、解が小さければ小さいほど指数関数的に長い時間、解が存在することは示せる。指数関数的に長い時間存在するならば永遠に存在するわけではなく、必ず有限時間で存在しなくなる点が数学的に重要だ。その研究結果が「方程式を満たす小さな解が、一意的かつ永遠に存在する」となる。その他、中村先生は宇宙論に関連するド・ジッター時空における非線形クライン・ゴルドン方程式や非線形シュレディンガー方程式の初期値問題にも取り組んでいる。
中村先生の研究室では、4年次には基礎的な研究方法の習熟に重点を置き、大学院生には自発的・主体的にひとつのことに集中して、限界まで追求し、その限界を一歩超すような経験が出来るようにと指導している。また、研究だけでなく、メールの書き方や先輩・研究者との接し方、立ち居振る舞いなど、人間的な成長にも心を砕いている。そして、有望な大学院生には国内外の研究集会に参加させて、先端研究に触れる機会が設けられている。
2018年3月には山形大学、東北大学、中国の北京大学との合同研究集会を理学部で行ったほか、7月には米国から相対論に基づく偏微分方程式論の研究者を招聘し、連続講演が行われる。数学は国際共同研究が多い分野で、競争的でチャレンジングな先端研究を肌で感じることは非常に意義深い。それが叶う環境という点も、本学理学部の強みと言える。

大学院生たちと討論する中村先生。学生たちに論文を読んできてもらい、わからないところを討論する授業スタイル。
「すぐに役立つものはすぐに役に立たなくなる」。この観点からすると、数学理論はすぐには役に立たないかもしれないが、将来的・持続的に役に立つ可能性が高い。株価、ビッグデータ、保険、通信暗号など、数学理論が役立つ分野が広がってきている。近年、企業もそれに気づき、数学理論に優れた人材を求める傾向が高まっている。自然現象や宇宙論、ビジネスにも通じる数学理論、どの入り口から足を踏み入れても様々な困難と大いなる喜びが待っていることだろう。
つづきを読む

なかむらまこと●教授/専門は関数方程式論。北海道出身。北海道大学大学院理学研究科博士後期課程修了。東北大学時代に「非線形双曲型偏微分方程式の初期値境界値問題の研究」で日本数学会建部賢弘特別賞を受賞。
※内容や所属等は2018年当時のものです。